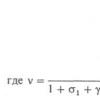Дисперсия альтернативного признака рассчитывается по формуле. Изучение формы распределения признака. Основные характеристики закономерностей распределения. Разделенной на группы
Основоположником развития теории средних величин является Адольф Кетле, который считал их важнейшими статистическими показателями. Он первым четко сформулировал тот факт, что на массовые явления (статистические совокупности) влияет два вида причин:
- общие для каждой единицы совокупности, эти причины формируют тип явления и связаны с его сущностью;
- индивидуальные, специфические для каждой единицы совокупности, не связанные с типом явления, то есть случайные для него.
При расчете средней величины в совокупности влияние случайных причин взаимопогашается, и средняя величина, абстрагируясь от индивидуальных особенностей отдельных единиц совокупности, выражает общие свойства, присущие всей совокупности. Кетле считал среднюю величину не просто статистическим показателем, имеющим определенный способ расчета, а категорией объективной реальности.
В настоящее время средняя величина признается также центральным показателем, характеризующим совокупность. И определяют ее как обобщающий показатель, характеризующий типический уровень варьирующего признака. Он выражает величину признака, отнесенную к единице совокупности.
Средняя всегда обобщает количественную вариацию признака, т.е. в средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами. В отличие от средней абсолютная величина, характеризующая уровень признака отдельной единицы совокупности, не позволяет сравнивать значения признака у единиц, относящихся к разным совокупностям. Так, если нужно сопоставить уровни оплаты труда работников на двух предприятиях, то нельзя сравнивать по данному признаку двух работников разных предприятий. Оплата труда выбранных для сравнения работников может быть не типичной для этих предприятий. Если же сравнивать размеры фондов оплаты труда на рассматриваемых предприятиях, то не учитывается численность работающих и, следовательно, нельзя определить, где уровень оплаты труда выше. В конечном итоге сравнить можно лишь средние показатели, т.е. сколько в среднем получает один работник на каждом предприятии. Таким образом, возникает необходимость расчета средней величины как обобщающей характеристики совокупности .
Вычисление среднего – один из распространенных приемов обобщения; средний показатель выделяет то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае.
Таким образом, в способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей. Следует отметить, что средняя величина будет объективной характеристикой, если она вычислена по качественно однородной совокупности.
Рассмотрим теперь виды средних величин, особенности их исчисления и области применения . Средние величины делятся на два больших класса: степенные средние и структурные средние.
К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая.
В качествеструктурных средних рассматриваются мода и медиана.
Выбор конкретного вида средней величины зависит от цели исследования и логической сущности усредняемого признака.
Степенные средние в зависимости от представления исходных данных могут быть простыми ивзвешенными .
Простая средняя считается по несгруппированным данным и имеет следующий общий вид:
где X
– варианта (значение) осредняемого признака;
m
– показатель степени средней;
n
– число вариант.
В зависимости от степени m получают различные виды средних величин.
Если же данные сгруппированы, то используется формулы средних взвешенных , где весами выступают частоты f (повторяемость варианты).
Взвешенная средня я считается по сгруппированным данным и имеет общий вид

где X –
варианта (значение) усредняемого признака или серединноезначение интервала, в котором измеряется варианта;
m
– показатель степени средней;
f
– частота, показывающая, сколько раз встречается каждое значение усредняемого признака.
Таблица 7. Виды степенных средних
| Вид степенной средней | Показатель степени (m) | Формула расчета | |
| Простая | Взвешенная | ||
| Гармоническая | -1 | ||
| Геометрическая |  |  |
|
| Арифметическая | |||
| Квадратическая | |||
| Кубическая |
Формулы средневзвешенные могут использоваться для расчета общей по совокупности средней на основе групповых средних.
Таблица 8. Оплата труда по бригадам
Таблица 9. Оплата труда по бригадам
В обеих задачах определяющей функцией является ФЗП.
Прежде, чем выбрать формулу для расчетов средней величины,нужно словами записать логическую сущность усредняемого признака.
Средняя заработная плата = Фонд заработной платы / численность работников
Средняя урожайность = Валовой сбор / Посевная площадь
Средняя производительность труда = Объем продукции / Численность (Время)
Правило: Если в представленной информации есть данные о числителе логической формулы, то есть об определяющей функции, то для расчета средней величины используется средняя гармоническая. Если представлены данные о знаменателе логической формулы, то для расчета средней величины используется средняя арифметическая.
Пример . В течение 8-часового рабочего дня пять рабочих производили одинаковые детали. Их затраты времени на одну деталь, мин.: 20, 16, 20, 15, 24. Определить средние затраты времени на одну деталь.
Средние затраты времени на одну деталь определяются путем деления суммарного времени на число деталей.
480 +480+480+480+480
480:20+480:16+480:20+480:15+480:24
(2400:130=18,46 мин.)
Это - правильный расчет, а неправильно, если сложить все затраты времени на одну деталь и разделить на пять (19 мин.). При таком расчете искажается объем производства деталей (2400:19=126, а не 130, как фактически).
1. Средняя арифметическая постоянной величины равна этой постоянной:
![]()
2. Алгебраическая сумма линейных отклонений варианты от средней арифметической равна 0 (нулевое свойство):
– для несгруппированных данных,
– для сгруппированных данных;
3. Сумма квадратов отклонений варианты от средней арифметической есть число минимальное:
– min (для несгруппированных данных),
– min (для сгруппированных данных);
Эти три свойства определяют сущность средней арифметической. Следующие свойства – расчетные .
4. Если каждую варианту Х уменьшить или увеличить на определенное число, то средняя величина уменьшается или увеличивается на это число.
5. Если каждую варианту Х уменьшить или увеличить в одно и то же число раз, то средняя величина уменьшается или увеличивается в это число раз.
6. Если каждую частоту f уменьшить или увеличить в одно и то же число раз, то средняя величина не изменится.

Доля каждой варианты (d) определяется путем деления каждой частоты на сумму всех частот.
Таким образом средняя величина зависит от варианты Х и от структуры совокупности, которая характеризуется долями d.
7. Средняя суммы равна сумме средних:
![]()
Ряд распределения имеет 3 центра:
1) средняя арифметическая;
3) медиана.
Рассчитаем среднюю арифметическую для дискретного ряда распределения, представленного в таблице 1:

При расчете средней величины по интервальному ряду распределения в качестве варианты Х берется середина интервала. Если интервал открытый, то при расчете средней величины его условно закрывают, принимая равным соседнему закрытому интервалу.
Рассчитаем среднюю величину основных средств по таблице 3:
Млрд.руб.
В таблице 5 была рассчитана эта же величина, и она получилась равной 3,3 млрд. руб. (Объяснить различия)
Мода – наиболее часто встречающаяся варианта.
Определим моду тарифного разряда по таблице 1:
Для интервальных рядов распределения сначала находится модальный интервал, то есть интервал с наибольшей частотой внутри этого интервала, затем мода находится по формуле:

Нижняя граница модального интервала;
i - величина модального интервала;
Частота модального интервала;
Частота интервала предшествующего модальному интервалу;
Частота интервала следующего за модальным интервалом.
![]() млрд. руб.
млрд. руб.
Медиана - варианта, стоящая в середине ряда распределения.
Номер медианы:
№ Ме= - если число единиц в совокупности четное;
№ Ме= - если число единиц в совокупности нечетное.
Найдем медиану тарифного разряда по таблице 1:
Следовательно, половина рабочих цеха имеет разряд не выше 3-го.
Прежде чем найти медиану для интервального ряда распределения, ищут интервал, в который входит срединная варианта, затем внутри этого интервала определяют медиану по формуле:
 ,
,
где - нижняя граница медианного интервала;
i- величина медианного интервала;
n- число единиц совокупности;
Накопленная частота интервала предшествующего медианному;
Частота медианного интервала
Найдем медиану основных средств по таблице 3:
 млрд.руб.,
млрд.руб.,
То есть половина предприятий имеет основные средства не выше, чем 3,45 млрд. руб.
Ряды распределения, имеющие одинаковую среднюю величину, могут существенно отличаться по степени колеблемости изучаемого признака. (Пример. Средний возраст студентов в группе и бабушки с детьми).
Для характеристики совокупности, особенно, в том случае, если значение признака существенно колеблется, дополнительно к расчету средней величины определяют ряд показателей вариации.
Для измерения вариации используют абсолютные и относительные показатели.
1. Размах вариации: R = X max – X min – диапазон изменения признака.
2. Среднее линейное отклонение – показывает среднее отклонение варианты от средней величины:
Для несгруппированных данных;

3. Среднее квадратическое отклонение - показывает среднее отклонение вариант от средней величины:
 - для не сгруппированных данных;
- для не сгруппированных данных;
 - для сгруппированных данных;
- для сгруппированных данных;
Все 3 показателя имеют те же единицы измерения, что и признак.
4. Дисперсия – квадрат среднего квадратического отклонения:

или 
Не имеет единиц измерения.
Свойства дисперсии :
1) D(const)=0, то есть дисперсия постоянной величины равна 0.
2) Если каждую варианту Х уменьшить или увеличить на одно и то же число раз, то дисперсия не изменится;
3) Если каждую варианту Х уменьшить или увеличить в одно и то же число раз i, то дисперсия уменьшится или увеличится в i 2 раз.
Способы расчета дисперсии:
1) исходя из определения: 
2) исходя из средней из квадратов вариант:
![]() ;
;  ;
;
Эта формула получена преобразованием основной формулы.
3) по способу моментов:
Первый условный момент;
Второй условный момент;
 ;
; 
Рассчитаем дисперсию тарифного разряда по данным таблицы 1 двумя способами:
2) ![]() =13,75-3,53=1,29
=13,75-3,53=1,29

Показатели относительного рассеивания (вариации) .
Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер вариации в различных распределениях (колеблемость одного и того же признака в двух совокупностях или колеблемость различных признаков в одной совокупности). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической.
1.Коэффициент осцилляции показывает относительную колеблемость крайних значений признака относительно средней.
![]()
2. Относительное линейное отклонение характеризует относительное усредненное значение абсолютных отклонений от средней величины.
![]()
3. Коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин.

В статистике совокупности, имеющие коэффициент вариации больше 30–35 %, принято считать неоднородными.
Для более глубокого анализа колеблемости признаков также используют показатели дифференциации.
1. По несгруппированным первичным данным можно рассчитать коэффициент фондовой дифференциации :
 ,
,
где - средняя величина, рассчитанная для 10% самых больших значений признака.
Средняя величина, рассчитанная для 10% самых маленьких значений признака.
2. Если данные сгруппированы, то рассчитывают коэффициент децильной дифференциации :
Где и - соответственно 1 и 9 децили.
Дециль - значение признака, которому в ряду распределения соответствует 10-я доля совокупности, то есть децили делят совокупность на 10 равных частей..
Процедура нахождения децилей аналогична процедуре нахождения медианы для интервального ряда распределения:
1) определяют № децили: для 1-й децили: № = ;
для 9-й децили: № = ;
2) находят интервалы, в которые входят эти децили и внутри этих интервалов находят децили по формулам:
 ;
;  ,
,
где и - соответственно нижние границы интервалов, в которые входят 1 и 9 децили;
i - величины интервалов, в которые входят 1 и 9 децили;
И - соответственно частоты интервалов, в которые входят 1 и 9 децили;
Накопленная частота интервала, предшествующая децильному (в первой формуле для 1-й децили, во второй формуле для 2-й децили).
Таблица 10. Распределение населения района
По среднедушевому доходу
| Месячный среднедушевой доход, тыс.руб | Численность | Накопленные частоты | |
| тыс.чел. | в % к итогу | ||
| 20-40 - 40-60 60-100 100-150 150-200 - 200-300 300-500 500 и выше | 9,2 25,2 32,9 30,0 27,4 15,5 4,9 3,1 | 6,2 17,0 22,2 20,2 18,5 10,5 3,3 2,1 | 9,2 () 34,4 () 67,3 97,3 124,7 () 140,2 () 145,1 148,2 |
| Итого | 148,2 | - |
Среди множества варьирующих признаков существуют признаки, которыми обладают одни единицы совокупности и не обладают другие. Эти признаки называются альтернативными. Например, ученая степень у преподавателя вуза. Вариация альтернативного признака качественно проявляется в значении нуля у единиц, которые этим признаком не обладают или в значении единицы у тех, которые данный признак имеют.
Пусть n – число единиц совокупности; m – число единиц совокупности, обладающих данным признаком; p – доля единиц, обладающих данным признаком (p=m/n); q - доля единиц, не обладающих данным признаком, причем p+q =1.
Альтернативный признак принимает всего два значения – 0 и 1 с весами соответственно q и p. Вычислим среднее значение альтернативного признака по формуле средней арифметической:
.
Дисперсия альтернативного признака определяется по формуле:
,
где R – среднеквадратическое отклонение альтернативного признака.
Вычислим дисперсию альтернативного признака по следующим данным: налоговой инспекций одного из районов города проверено 86 коммерческих киосков и в 37 обнаружены финансовые нарушения. Тогда
Следовательно, дисперсия и среднее квадратическое отклонение доли коммерческих киосков, имеющих финансовые нарушения, во всей совокупности обследованных киосков равны:
Обобщенной характеристикой различий внутри ряда может служить энтропия распределения. Применительно к статистике энтропия – это мера неопределенности данных наблюдения, которая может иметь различные результаты.

Показатель энтропии (Hx):
 ,
,
где p i
– вероятность события x i .
Расчет энтропии распределения можно показать на примере выпуска продукции различных сортов на одном из предприятий точного машиностроения (табл. 5.4).
Таблица 5.4 - Вероятности различных сортов продукции
Среди множества варьирующих признаков, изучаемых статистикой, существуют признаки, которыми обладают одни единицы совокупности и не обладают другие. Эти признаки называются альтернативными . Примером таких признаков являются наличие бракованной продукции, ученая степень преподавателя вуза, учеба по определенной специальности и т. д.
Предположим, что вся статистическая совокупность имеет n единиц. Из нихm единиц обладают выделенным признаком, тогда оставшиесяn –m единиц не обладают этим признаком.
Долю единиц, обладающих признаком,
обозначим:
,
тогда пусть –
доля единиц, не обладающих данным
признаком.
–
доля единиц, не обладающих данным
признаком.
р + q = 1
Единицам х, обладающим данным признаком, присвоим значениех = 1, а не обладающим –х = 0.
Среднее значение альтернативного признака :
 =р.
=р.
То есть среднее значение альтернативного признака равно доле единиц, обладающих данным признаком.
Дисперсия альтернативного признака :
То есть дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, на долю единиц, не обладающих данным признаком.
Пример:
5% изготовленных изделий
– брак, тогда 95% изделий годных. Дисперсия
доли брака равна: σ 2 = 0,050,95
= 0,0475, а среднее квадратическое отклонение
доли брака составляет σ = или 22%.
или 22%.
Предельное значение дисперсии альтернативного признака равно 0,25; оно получается при р =q = 0,5.
3. Дисперсионный анализ
Вариация признака обусловлена различными факторами, некоторые из этих факторов можно выделить, если статистическую совокупность разбить на группы по какому-либо признаку. Тогда, наряду с изучением вариации признака по всей совокупности в целом, становится возможным изучить вариацию для каждой из составляющих ее группы, а также и между этими группами. В простейшем случае, когда совокупность расчленена на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трех видов дисперсий:общей , межгрупповой и внутригрупповой .
Общая
дисперсия
σ
2
общ
измеряет
вариацию признака по всей совокупности
под влиянием всех факторов, обусловивших
эту
вариацию. Она равна среднему квадрату
отклонений отдельных значений
признака х
от
общей по совокупности средней
 и может быть вычислена
по формуле простой
или
взвешен
ной
дисперсии.
и может быть вычислена
по формуле простой
или
взвешен
ной
дисперсии.
Межгрупповая
дисперсия
σ
2
межгр
характеризует
систематическую вариацию
результативного признака, обусловленную
влиянием признака-фактора,
положенного в основание группировки.
Она равна
среднему квадрату отклонений групповых
(частных) средних
 от общей средней
от общей средней :
:
σ 2 межгр =
 ,
,
где f - численность единиц в группе.
Внутригрупповая
(частная) дисперсия
σ
2
i
отражает случайную вариацию,
т. е. часть вариации, обусловленную
влиянием неучтенных
факторов и не зависящую от признака-фактора,
положенного в
основание группировки. Она равна
среднему квадрату отклонений
отдельных значений признака внутри
группы х
от
средней арифметической
этой группы
 (групповой средней) и может быть
исчислена по формуле простой
или взвешенной
дисперсии
:
(групповой средней) и может быть
исчислена по формуле простой
или взвешенной
дисперсии
:
σ 2 i
=
 (простая формула);
(простая формула);
σ 2 i
=
 (взвешенная).
(взвешенная).
На основании внутригрупповой дисперсии по каждой группе (σ 2 i ) можно определить общую средн юю из внутригрупповых дисперсий :
 =
=
 .
.
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:
σ 2 общ = σ 2 межгр +
 .
.
Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью - неизвестную, а также судить о силе влияния группировочного признака.
Чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый признак.
В статистическом анализе широко используется эмпирический коэффициент детерминации (η 2) - показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:
η 2
=
 .
.
Эмпирический коэффициент детерминации показывает долю вариации результативного признака у под влиянием факторного признака х (остальная часть общей вариации у обусловливается вариацией прочих факторов). При отсутствии связи эмпирический коэффициент детерминации η 2 равен нулю, а при функциональной связи - единице. Если, например η 2 = 0,666, это значит, что на 66,6% вариация исследуемого показателя обусловлена различиями в значениях признака-фактора, положенного в основание группировки, и на 33,4% - влиянием прочих факторов.
Эмпирическое корреляционное отношение - это корень квадратный из эмпирического коэффициента детерминации:
η =
 .
.
Оно показывает тесноту связи между группировочным и результативным признаками.
Эмпирическое корреляционное отношение η, как и η 2 , может принимать значения от 0 до 1.
Если связь отсутствует, то корреляционное отношение η = 0, т. е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации.
Если связь функциональная, то корреляционное отношение η = 1. В этом случае межгрупповая дисперсия равна общей дисперсии (σ 2 межгр = σ 2), т. е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака.
Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.
Среднее значение альтернативного признака и его дисперсия:
Среднее значение альтернативного признака
Дисперсия альтернативного признака
Подставив в формулу дисперсииq = 1 – p , получим:
![]()
Таким образом, дисперсия альтернативного признака равна произведению доли единиц , обладающих данным признаком и доли единиц, не обладающих данным признаком.
Среднее квадратическое отклонение альтернативного признака:
![]()
Вариация альтернативного признака заключается в наличии или отсутствии изучаемого свойства у единиц совокупности. Количественно вариация альтернативного признака выражается двумя значениями: наличие у единицы изучаемого свойства обозначается единицей (1), а его отсутствие - нулем (0). Долю единиц, обладающих изучаемым признаком, обозначают буквой , а долю единиц, не обладающих этим признаком - через . Учитывая, что p + q = 1 (отсюда q = 1 - p), а среднее значение альтернативного признака равно
![]() ,
,
средний квадрат отклонений 
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным свойством (), на долю единиц, данным свойством не обладающих ().
Максимальное значение средний квадрат отклонения (дисперсия) принимает в случае равенства долей, т.е. когда т.е. . Нижняя граница этого показателя равна нулю, что соответствует ситуации, при которой в совокупности отсутствует вариация. Среднее квадратическое отклонение альтернативного признака:
![]()
Выборочное наблюдение, преимущества и недостатки.
Выборочное наблюдение – одно из наиболее современных видов статистического наблюдения, при котором обследованию подвергается часть единиц изучаемой совокупности, отобранных на основе научно разработанных принципов, обеспечивающих получение достаточного количества достоверных данных, для того чтобы охарактеризовать всю совокупность в целом.
Средние и относительные показатели, полученные на основе выборочных данных, должны достаточно полно воспроизводить соответствующие показатели совокупности в целом.
Основные преимущества выборочного наблюдения в том, что его можно осуществить по более широкой программе, оно более дешевое с точки зрения затрат на его проведение, и его можно организовать тогда и в тех случаях, когда отчетностью мы воспользоваться не можем.
Основными недостатками является то, что полученные данные всегда содержат в себе ошибку, и о результатах наблюдения можно судить лишь с определенной степенью достоверности. А также для его проведения требуются квалифицированные кадры.
Способы формирование выборочной совокупности.
В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения.
Основным условием проведения выборочного обследования является предупреждение возникновения систематических ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности. Предупреждение систематических ошибок достигается в результате применения научно обоснованных способов формирования выборочной совокупности.
Существуют следующие способы отбора единиц из генеральной совокупности:
1) индивидуальный отбор - в выборку отбираются отдельные единицы;
2) групповой отбор - в выборку попадают качественно однородные группы или серии изучаемых единиц;
3) комбинированный отбор - это комбинация индивидуального и группового отбора.
Способы отбора определяются правилами формирования выборочной совокупности.
Выборка может быть:
Собственно-случайная состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки. Доля выборки есть отношение числа единиц выборочной совокупности n к численности единиц генеральной совокупности N, т.е.
§ механическая состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки. Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке - каждая 20-я единица (1:0,05) и т.д. Таким образом, в соответствии с принятой долей отбора, генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой группы в выборку отбирается лишь одна единица.
§ типическая – при которой генеральная совокупность вначале расчленяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Важной особенностью типической выборки является то, что она дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность;
§ серийная - при которой генеральную совокупность делят на одинаковые по объему группы - серии. В выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию;
Комбинированная - выборка может быть двухступенчатой. При этом генеральная совокупность сначала разбивается на группы. Затем производят отбор групп, а внутри последних осуществляется отбор отдельных единиц.
В статистике различают следующие способы отбора единиц в выборочную совокупность:
§ одноступенчатая выборка - каждая отобранная единица сразу же подвергается изучению по заданному признаку (собственно-случайная и серийная выборки);
Многоступенчатая выборка - производят подбор из генеральной совокупности отдельных групп, а из групп выбираются отдельные единицы (типическая выборка с механическим способом отбора единиц в выборочную совокупность).
Кроме того различают:
§ повторный отбор – по схеме возвращенного шара. При этом каждая попавшая в выборку единица иди серия возвращается в генеральную совокупность и поэтому имеет шанс снова попасть в выборку;
Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности. Исследование вариации имеет большое практическое значение и является необходимым звеном в экономическом анализе. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию.
Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей.
Абсолютные показатели вариации включают:
Размах вариации (R)
Размах вариации — это разность между максимальным и минимальным значениями признака
Он показывает пределы, в которых изменяется величина признака в изучаемой .
Пример
. Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.
Решение: размах вариации = 9 — 2 = 7 лет.
Для обобщенной характеристики различий в значениях признака вычисляют средние показатели вариации, основанные на учете отклонений от средней арифметической. За отклонение от средней принимается разность .
При этом во избежании превращения в нуль суммы отклонений вариантов признака от средней (нулевое свойство средней) приходится либо не учитывать знаки отклонения, то есть брать эту сумму по модулю , либо возводить значения отклонений в квадрат
Среднее линейное и квадратическое отклонение
Среднее линейное отклонение — это из абсолютных отклонений отдельных значений признака от средней.
Среднее линейное отклонение простое:
Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.
В нашем примере: лет;
Ответ: 2,4 года.
Среднее линейное отклонение взвешенное применяется для сгруппированных данных:
Среднее линейное отклонение в силу его условности применяется на практике сравнительно редко (в частности, для характеристики выполнения договорных обязательств по равномерности поставки; в анализе качества продукции с учетом технологических особенностей производства).
Среднее квадратическое отклонение
Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). () равно квадратному корню из среднего квадрата отклонений отдельных значений признака от :
Среднее квадратическое отклонение простое:


Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:

Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение: ~ 1,25.
Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.
Дисперсия
Дисперсия - представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.
Дисперсия простая:
В нашем примере:
Дисперсия взвешенная:
Более удобно вычислять дисперсию по формуле:
![]()
которая получается из основной путем несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней.
Для несгрупиированных данных:

Для сгруппированных данных:

Вариация альтернативного признака заключается в наличии или отсутствии изучаемого свойства у единиц совокупности. Количественно вариация альтернативного признака выражается двумя значениями: наличие у единицы изучаемого свойства обозначается единицей (1), а его отсутствие — нулем (0). Долю единиц, обладающих изучаемым признаком, обозначают буквой , а долю единиц, не обладающих этим признаком — через . Учитывая, что p + q = 1 (отсюда q = 1 — p), а среднее значение альтернативного признака равно
![]() ,
,
средний квадрат отклонений

Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным свойством (), на долю единиц, данным свойством не обладающих ().
Максимальное значение средний квадрат отклонения (дисперсия) принимает в случае равенства долей, т.е. когда т.е. . Нижняя граница этого показателя равна нулю, что соответствует ситуации, при которой в совокупности отсутствует вариация. Среднее квадратическое отклонение альтернативного признака:
![]()
Так, если в изготовленной партии 3% изделий оказались нестандартными, то дисперсия доли нестандартных изделий , а среднее квадратическое отклонение или 17,1%.
Среднее квадратическое отклонение равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической.
Относительные показатели вариации
Относительные показатели вариации включают:
Сравнение вариации нескольких совокупностей по одному и тому же признаку, а тем более по различным признакам с помощью абсолютных показателей не представляется возможным. В этих случаях для сравнительной оценки степени различия строят относительные показатели вариации. Они вычисляются как отношения абсолютных показателей вариации к средней:
Рассчитываются и другие относительные характеристики. Например, для оценки вариации в случае асимметрического распределения вычисляют отношение среднего линейного отклонения к медиан
так как благодаря свойству медианы сумма абсолютных отклонений признака от ее величины всегда меньше, чем от любой другой.
В качестве относительной меры рассеивания, оценивающей вариацию центральной части совокупности, вычисляют относительное квартильное отклонение , где — средний квартиль полусуммы разности третьего (или верхнего) квартиля () и первого (или нижнего) квартиля ().
На практике чаще всего вычисляют коэффициент вариации. Нижней границей этого показателя является нуль, верхнего предела он не имеет, однако известно, что с увеличением вариации признака увеличивается и его значение. Коэффициент вариации является в известном смысле критерием однородности совокупности (в случае нормального распределения).
Рассчитаем коэффициент вариации на основе среднего квадратического отклонения для следующего примера. Расход сырья на единицу продукции составил (кг): по одной технологии при , а по другой — при. Непосредственное сравнение величины средних квадратических отклонений могло бы привести к неверному представлению о том, что вариация расхода сырья по первой технологии интенсивнее, чем по второй (. Относительная мера вариации ( позволяет сделать противоположный вывод
Пример расчета показателей вариацииНа этапе отбора кандидатов для участия в осуществлении сложного проекта фирма объявлила конкурс профессионалов. Распределение претендентов по опыту работы показало средующие результаты:

Вычислим средний производственный опыт работы, лет

Рассчитаем дисперсию по продолжительности опыта работы

Такой же результат получается, если использовать для расчета другую формулу расчета дисперсии

Вычислим среднее квадратическое отклонение, лет:
Определим коэффициент вариации, %:
Правило сложения дисперсий
Для оценки влияния факторов, определяющих вариацию, используют прием группировки: совокупность разбивают на группы, выбрав в качестве группировочного признака один из определяющих факторов. Тогда наряду с общей дисперсией, рассчитанной по всей совокупности, вычисляют внутигрупповую дисперсию (или среднюю из групповых) и межгрупповую дисперсию (или дисперсию групповых средних).
Общая дисперсия характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий.
Межгрупповая дисперсия измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:

Внутригрупповая дисперсия оценивает вариацию признака, сложившуюся по влиянием других, неучитываемых в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий.

Все три дисперсии () связаны между собой следующим равенством, которое известно как правило сложения дисперсий:
на этом соотношении строятся показатели, оценивающие влияние признака группировки на образование общей вариации. К ним относятся эмпирический коэффициент детерминации () и эмпирическое корреляционное отношение ()
() характеризует долю межгрупоовой дисперсии в общей дисперсии:
и показывает насколько вариация признака в совокупности обусловлена фактором группировки.
Эмпирическое корреляционное отношение (!!\eta = \sqrt{ \frac{\delta^2}{\sigma^2} }
оценивает тесноту связи между изучаемым и группировочным признаками. Предельными значениями являются нуль и единица. Чем ближе к единице, тем теснее связь.
Пример. Стоимость 1 кв.м общей площади (усл.ед) на рынке жилья по десяти 17-м домам улучшенной планировки составляла:

При этом известно, что первые пять домов были построены вблизи делового центра, а остальные — на значительном расстоянии от него.
Для рассчета общей дисперсии вычислим среднюю стоимость 1 кв.м. общей площади: Общую дисперсию определим по формуле![]() :
:
Вычислим среднюю стоимость 1 кв.м. и дисперсию по этому показателю для каждой группы домов, отличающихся месторасположением относительно центра города:
а) для домов, построенных вблизи центра:
б) для домов, построенных далеко от центра:
Вариация стоимости 1 кв.м. общей площади, вызванная изменением местоположения домов, определяется величиной межгрупповой дисперсии :
Вариация стоимости 1 кв.м. общей площади, обусловленная изменением остальных неучитываемых нами показателей, измеряется величиной внутригрупповой дисперсии
Найденные дисперссии в сумме дают величину общей дисперсии
Эмпирический коэффициент детерминации :
показывает, что дисперсия стоимости 1.кв.м. общей площади на рынке жилья на 81,8% объясняется различиями в расположении новостроек по отношению к деловому центру и на 18,2% — другими факторами.
Эмприческое корреляционное отношение свидетельствует о существенном влиянии на стоимость жилья месторасположения домов.
Правило сложения дисперсий для доли
признака записывается так:![]()
а три вида дисперсий доли для сгруппированных данных определяется по следующим формулам:
общая дисперсия:![]()

Формулы межгрупповой и внутригрупповой дисперсий:

Характеристики формы распределения
Для получения представления о форме распределения используются показатели среднего уровня ( , ), показатели вариации, ассиметрии и эксцесса.
В симметричных распределениях средняя арифметическая, мода и медиана совпадают (. Если это равенство нарушается — распределение ассиметрично.
Простейшим показателем ассиметрии является разность , которая в случае правосторонней ассиметрии положительна, а при левосторонней — отрицательна.
Ассиметричное распределение
Для сравнения ассиметрии нескольких рядов вычисляется относительный показатель
В качестве обобщающих характеристик вариации используются центральные моменты распределения -го порядка , соответствующие степени, в которую возводятся отклонения отдельных значений признака от средней арифметической:
Для несгруппированных данных:

Для сгруппированных данных:

Момент первого порядка согласно свойству средней арифметической равен нулю .
Момент второго порядка является дисперсией .
Моменты третьего и четвертого порядков используются для построения показателей, оценивающих особенности формы эмпирических распределений.
С помощью момента третьего порядка измеряют степень скошенности или ассиметричности распределения.
— коэффициент ассиметрии
В симметричных распределениях , как все центральные моменты нечетного порядка.Неравенство нулю центрального момента третьего порядка указывает на асимметричность распределения. При этом, если , то асимметрия правосторонняя и относительно максимальной ординаты вытянута правая ветвь; если , то асимметрия левосторонняя (на графике это соответствует вытянутости левой ветви).
Для характеристики островершинности или плосковершинности распределения вычисляют отношение момента четвертого порядка () к среднеквадратическому отклонению в четвертой степени (). Для нормального распределения , поэтому эксцесс находят по формуле:
Для нормального распределения обращается в нуль. Для островершинных распределений , для плосковершинных .
Эксцесс распределения
Кроме показателей, рассмотренных выше, обобщающей характеристикой вариации в однородной совокупности служит определенный порядок в изменении частот распределения в соответствии с изменениями величины изучаемого признака, называемый закономерностью распределения .
Характер (тип) закономерности распределения может быть выявлен путем построения вариационного ряда на основании большого объема наблюдений, а также такого выбора числа групп и величины интегралов, при котором наиболее отчетливо могла бы проявиться закономерность.
Анализ вариационных рядов предполагает выявление характера распределения (как результата действия механизма вариации), установление функции распределения, проверку соответствия эмпирического распределения теоретическому.
Эмпирическое распределение , полученное на основе данных наблюдения, графически изображается эмпирической кривой распределения с помощью полигона.
На практике встречаются различные типы распределений, среди которых можно выделить симметричные и асимметричные, одновершинные и многовершинные.
Установить тип распределения, означает выразить механизм формирования закономерности в аналитической форме. Многим явлениям и их признакам свойственны характерные формы распределения, которые аппроксимируются соответствующими кривыми. При всем многообразии форм распределения наибольшее распространение в качестве теоретических получили нормальное распределение, распределение Пауссона, биноминальное распределение и др.
Особое место в изучении вариации принадлежит нормальному закону, благодаря его математическим свойствам. Для нормального закона выполняется правило трех сигм, по которому вариация индивидуальных значений признака находится в пределах от величины средней. При этом в границах находится около 70% всех единиц, а в пределах — 95%.
Оценка соответствия эмпирического и теоретического распределений производится с помощью критериев согласия, среди которых широко известны критерии Пирсона, Романовского, Ястремского, Колмогорова.