На этом уроке будем учиться устанавливать непрерывность функции. Будем делать это с помощью пределов, причем односторонних - правого и левого, которые совсем не страшны, несмотря на то что записываются как и .

Но что такое вообще непрерывность функции? Пока мы не дошли до строгого определения, проще всего представить себе линию, которую можно начертить, не отрывая карандаш от бумаги. Если такая линия начерчена, то она непрерывна. Эта линия и является графиком непрерывной функции.

Графически функция непрерывна в точке , если её график не "разрывается" в этой точке. График такой непрерывной функции - показан на рисунке ниже.

Определение непрерывности функции через предел. Функция является непрерывной в точке при соблюдении трёх условий:

1. Функция определена в точке .

Если хотя бы одно из перечисленных условий не соблюдено, функция не является непрерывной в точке. При этом говорят, что функция терпит разрыв, а точки на графике, в которых график прерывается, называются точками разрыва функции. График такой функции , терпящей разрыв в точке x=2 - на рисунке ниже.

Пример 1. Функция f (x ) определена следующим образом:

Будет ли эта функция непрерывной в каждой из граничных точек её ветвей, то есть в точках x = 0 , x = 1 , x = 3 ?

Решение. Проверяем все три условия непрерывности функции в каждой граничной точке. Первое условие соблюдается, так как то, что функция определена в каждой из граничных точек, следует из определения функции. Осталось проверить остальные два условия.

Точка x = 0 . Найдём левосторонний предел в этой точке:

.

Найдём правосторонний предел:

x = 0 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

Как видим, предел функции и значение функции в точке x = 0 равны. Следовательно, функция является непрерывной в точке x = 0 .

Точка x = 1 . Найдём левосторонний предел в этой точке:

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 1 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

.

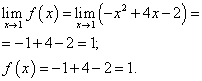Предел функции и значение функции в точке x = 1 равны. Следовательно, функция является непрерывной в точке x = 1 .

Точка x = 3 . Найдём левосторонний предел в этой точке:

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 3 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

.

Предел функции и значение функции в точке x = 3 равны. Следовательно, функция является непрерывной в точке x = 3 .

Основной вывод: данная функция является непрерывной в каждой граничной точке.

Что такое непрерывное изменение функции?

Непрерывное изменение функции можно определить как изменение постепенное, без скачков, при котором малое изменение аргумента влечёт малое изменение функции .

Проиллюстрируем это непрерывное изменение функции на примере.

Пусть над столом висит на нитке груз. Под действием этого груза нитка растягивается, поэтому расстояние l груза от точки подвеса нити является функцией массы груза m , то есть l = f (m ) , m ≥0 .

Если немного изменить массу груза, то расстояние l изменится мало: малым изменениям m соответствуют малые изменения l . Однако если масса груза близка к пределу прочности нити, то небольшое увеличение массы груза может вызвать разрыв нити: расстояние l скачкообразно увеличится и станет равным расстоянию от точки подвеса до поверхности стола. График функции l = f (m ) изображён на рисунке. На участке этот график является непрерывной (сплошной) линией, а в точке он прерывается. В результате получается график, состоящий из двух ветвей. Во всех точках, кроме , функция l = f (m ) непрерывна, а в точке она имеет разрыв.

Исследование функции на непрерывность может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графика .

Непрерывность функции на промежутке

Пусть функция y = f (x ) определена в интервале ]a , b [ и непрерывна в каждой точке этого интервала. Тогда она называется непрерывной в интервале ]a , b [ . Аналогично определяется понятие непрерывности функции на промежутках вида ]- ∞, b [ , ]a , + ∞[ , ]- ∞, + ∞[ . Пусть теперь функция y = f (x ) определена на отрезке [a , b ] . Разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок. Здесь следует упомянуть о так называемой односторонней непрерывности: в точке a , оставаясь на отрезке [a , b ] , мы можем приближаться только справа, а к точке b - только слева. Функция называется непрерывной на отрезке [a , b ] , если она непрерывна во всех внутренних точках этого отрезка, непрерывна справа в точке a и непрерывна слева в точке b .

Примером непрерывной функции может служить любая из элементарных функций. Каждая элементарная функция непрерывна на любом отрезке, на котором она определена. Например, функции и непрерывны на любом отрезке [a , b ] , функция непрерывна на отрезке [0 , b ] , функция непрерывна на любом отрезке, не содержащем точку a = 2 .

Пример 4. Исследовать функцию на непрерывность.

Решение. Проверяем первое условие. Функция не определена в точках - 3 и 3. По меньшей мере одно из условий непрерывности функции на всей числовой прямой не выполняется. Поэтому данная функция является непрерывной на интервалах

.

Пример 5. Определить, при каком значении параметра a непрерывна на всей области определения функция

Решение.

Найдём правосторонний предел при :

.

Очевидно, что значение в точке x = 2 должно быть равно ax :

a = 1,5 .

Пример 6. Определить, при каких значениях параметров a и b непрерывна на всей области определения функция

Решение.
Найдём левосторонний предел функции в точке :

.

Следовательно, значение в точке должно быть равно 1:

Найдём левосторонний функции в точке :

Очевидно, что значение функции в точке должно быть равно :

Ответ: функция непрерывна на всей области определения при a = 1; b = -3 .

Основные свойства непрерывных функций

К понятию непрерывной функции математика пришла, изучая в первую очередь различные законы движения. Пространство и время бесконечны, и зависимость, например, пути s от времени t , выраженная законом s = f (t ) , даёт пример непрерывной функции f (t ) . Непрерывно изменяется и температура нагреваемой воды, она также является непрерывной функцией от времени: T = f (t ) .

В математическом анализе доказаны некоторые свойства, которыми обладают непрерывные функции. Приведём важнейшие из этих свойств.

1. Если непрерывная на интервале функция принимает на концах интервала значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю. В более формальном изложении это свойство дано в теореме, известной как первая теорема Больцано-Коши.

2. Функция f (x ) , непрерывная на интервале [a , b ] , принимает все промежуточные значения между значениями в концевых точках, то есть, между f (a ) и f (b ) . В более формальном изложении это свойство дано в теореме, известной как вторая теорема Больцано-Коши.

Определение непрерывности по Гейне

Говорят, что функция действительного переменного \(f\left(x \right)\) является непрерывной в точке \(a \in \mathbb{R}\) (\(\mathbb{R}-\)множество действительных чисел), если для любой последовательности \(\left\{ {{x_n}} \right\}\), такой, что \[\lim\limits_{n \to \infty } {x_n} = a,\] выполняется соотношение \[\lim\limits_{n \to \infty } f\left({{x_n}} \right) = f\left(a \right).\] На практике удобно использовать следующие \(3\) условия непрерывности функции \(f\left(x \right)\) в точке \(x = a\) (которые должны выполняться одновременно):

1. Функция \(f\left(x \right)\) определена в точке \(x = a\);
2. Предел \(\lim\limits_{x \to a} f\left(x \right)\) существует;
3. Выполняется равенство \(\lim\limits_{x \to a} f\left(x \right) = f\left(a \right)\).

Определение непрерывности по Коши (нотация \(\varepsilon - \delta\))

Рассмотрим функцию \(f\left(x \right)\), которая отображает множество действительных чисел \(\mathbb{R}\) на другое подмножество \(B\) действительных чисел. Говорят, что функция \(f\left(x \right)\) является непрерывной в точке \(a \in \mathbb{R}\), если для любого числа \(\varepsilon > 0\) существует число \(\delta > 0\), такое, что для всех \(x \in \mathbb{R}\), удовлетворяющих соотношению \[\left| {x - a} \right| Определение непрерывности в терминах приращений аргумента и функции

Определение непрерывности можно также сформулировать, используя приращения аргумента и функции. Функция является непрерывной в точке \(x = a\), если справедливо равенство \[\lim\limits_{\Delta x \to 0} \Delta y = \lim\limits_{\Delta x \to 0} \left[ {f\left({a + \Delta x} \right) - f\left(a \right)} \right] = 0,\] где \(\Delta x = x - a\).

Приведенные определения непрерывности функции эквивалентны на множестве действительных чисел.

Функция является непрерывной на данном интервале , если она непрерывна в каждой точке этого интервала.

Теоремы непрерывности

Теорема 1.
Пусть функция \(f\left(x \right)\) непрерывна в точке \(x = a\) и \(C\) является константой. Тогда функция \(Cf\left(x \right)\) также непрерывна при \(x = a\).

Теорема 2.
Даны две функции \({f\left(x \right)}\) и \({g\left(x \right)}\), непрерывные в точке \(x = a\). Тогда сумма этих функций \({f\left(x \right)} + {g\left(x \right)}\) также непрерывна в точке \(x = a\).

Теорема 3.
Предположим, что две функции \({f\left(x \right)}\) и \({g\left(x \right)}\) непрерывны в точке \(x = a\). Тогда произведение этих функций \({f\left(x \right)} {g\left(x \right)}\) также непрерывно в точке \(x = a\).

Теорема 4.
Даны две функции \({f\left(x \right)}\) и \({g\left(x \right)}\), непрерывные при \(x = a\). Тогда отношение этих функций \(\large\frac{{f\left(x \right)}}{{g\left(x \right)}}\normalsize\) также непрерывно при \(x = a\) при условии, что \({g\left(a \right)} \ne 0\).

Теорема 5.
Предположим, что функция \({f\left(x \right)}\) является дифференцируемой в точке \(x = a\). Тогда функция \({f\left(x \right)}\) непрерывна в этой точке (т.е. из дифференцируемости следует непрерывность функции в точке; обратное − неверно).

Теорема 6 (Теорема о предельном значении).
Если функция \({f\left(x \right)}\) непрерывна на закрытом и ограниченном интервале \(\left[ {a,b} \right]\), то она ограничена сверху и снизу на данном интервале. Другими словами, существуют числа \(m\) и \(M\), такие, что \ для всех \(x\) в интервале \(\left[ {a,b} \right]\) (рисунок 1).

Рис.1		Рис.2

Теорема 7 (Теорема о промежуточном значении).
Пусть функция \({f\left(x \right)}\) непрерывна на закрытом и ограниченном интервале \(\left[ {a,b} \right]\). Тогда, если \(c\) − некоторое число, большее \({f\left(a \right)}\) и меньшее \({f\left(b \right)}\), то существует число \({x_0}\), такое, что \ Данная теорема проиллюстрирована на рисунке 2.

Непрерывность элементарных функций

Все элементарные функции являются непрерывными в любой точке свой области определения.

Функция называется элементарной , если она построена из конечного числа композиций и комбинаций
(с использованием \(4\) действий - сложение, вычитание, умножение и деление) . Множество основных элементарных функций включает в себя:

Учреждение образования «Белорусская государственная

сельскохозяйственная академия»

Кафедра высшей математики

Методические указания

по изучению темы «Непрерывность функций одной переменной»

студентами бухгалтерского факультета заочной формы получения

образования (НИСПО)

Горки, 2013

Непрерывность функций одной переменной

Односторонние пределы

Пусть функция
определена на множестве
. Введём понятие односторонних пределов функции при
. Будем рассматривать такие значения х , что
. Это означает, что
, оставаясь всё время слева от
при
то он называется левым пределом этой функции в точке (или при
) и обозначается

.

Пусть теперь
, оставаясь всё время справа от , т.е. оставаясь больше . Если при этом существует предел функции
, то он называется правым пределом этой функции в точке и обозначается

.

Левый и правый пределы называются односторонними пределами функции в точке.

Если существуют односторонние пределы функции в точке и они равны между собой, то функция имеет тот же предел в этой точке :

.

Если односторонние пределы функции в точке существуют, но не равны между собой, то предел функции в этой точке не существует .

Непрерывность функции в точке

Пусть функция
определена на некотором множестве D . Пусть независимая переменная х переходит от одного своего (начального) значения
к другому (конечному) значению . Разность конечного и начального значений называется приращением величины х и обозначается
. Приращение может быть как положительным, так и отрицательным. В первом случае величина х при переходе от к х увеличивается, а во втором случае - уменьшается.

Если независимая переменная х получает некоторое приращение
, то функция
получает приращение
. Так как
, то .

Приращением функции
в точке называется разность , где
– приращение независимой переменной.

Можно дать несколько определений непрерывности функции в точке.

Функция называется непрерывной в интервале , если она непрерывна в каждой точке этого интервала. Геометрически непрерывность функции
в замкнутом интервале означает, что график функции представляет собой сплошную линию без разрывов.

Непрерывные на отрезке функции обладают важными свойствами, которые выражаются следующими утверждениями.

Если функция
непрерывна на отрезке [a , b ], то она ограничена на этом отрезке.

Если функция
непрерывна на отрезке [a , b ], то она достигает на этом отрезке своего наименьшего и наибольшего значений.

Если функция
непрерывна на отрезке [a , b ] и
, то каким бы ни было число С , заключённое между числами А и В , найдётся точка
, что
.

Из этого утверждения следует, что если функция
непрерывна на [a , b ] и на концах этого отрезка принимает значения разных знаков, то на этом отрезке существует хотя бы одна точка c , в которой функция обращается в нуль.

Справедливо следующее утверждение: если над непрерывными функциями производить арифметические действия, то в результате получается непрерывная функци я.

Пример 1 .

в точке
.

Решение . Значение функции при
есть
. Вычислим односторонние пределы функции в точке
:

Так как односторонние пределы при
равны между собой и равны значению функции в этой точке, то данная функция непрерывна в точке
.

3. Непрерывность элементарных функций

Рассмотрим функцию
. Эта постоянная функция непрерывна в любой точке , так как
.

Функция
также непрерывна в каждой точке
, так как
. Так как
, то на основании приведённого утверждения об арифметических операциях над непрерывными функциями
будет непрерывной. Непрерывными будут такжен функции
.

Аналогично можно показать непрерывность остальных элементарных функций.

Таким образом, любая элементарная функция непрерывна в своей области определения, т.е. область определения элементарной функции совпадает с областью её непрерывности.

Непрерывность сложной и обратной функций

Пусть функция
непрерывна в точке , а функция
непрерывна в точке
. Тогда сложная функция
непрерывна в точке . Это означает, что если сложная функция составлена из непрерывных функций, то она также будет непрерывной, т.е. непрерывная функция от непрерывной функции есть функция непрерывная . Это определение распространяется на конечное число непрерывных функций.

Из этого определения следует, что под знаком непрерывной функции можно переходить к пределу:

Это означает, что если функция непрерывна, то знак предела и знак функции можно поменять местами.

Пусть функция
a , b ]. Тогда обратная ей функция
определена, строго монотонна и непрерывна на отрезке [A , B ], где
.

Точки разрыва и их классификаци я

Как уже известно, что если функция
определена на множестве D и в точке
выполняется условие
, то функция непрерывна в этой точке. Если же это условие непрерывности не выполняется, то в точке х 0 функция имеет разрыв.

Точка называется точкой разрыва первого рода функции
, если в этой точке функция имеет конечные односторонние пределы, не равные друг другу, т.е. . При этом величина

называется скачком функции
в точке .

Точка называется точкой устранимого разрыва функции
, если односторонние пределы функции в этой точке равны друг другу и не равны значению функции в этой точке, т.е. В этом случае для устранения разрыва в точке нужно положить

Точка х 0 называется точкой разрыва второго рода функции
если хотя бы один из односторонних пределов
или
в этой точке либо не существует, либо равен бесконечности.

Пример 2 . Исследовать на непрерывность функцию

.

Решение . Функция определена и непрерывна на всей числовой прямой, за исключением точки
. В этой точке функция имеет разрыв. Найдём односторонние пределы функции в точке
:

Так как в точке
односторонние пределы равны между собой, а функция в этой точке не определена, то точка
является точкой устранимого разрыва. Чтобы устранить разрыв в этой точке, необходимо доопределить функцию, положив
.

Пример 3 . Исследовать на непрерывность функцию

.

Решение . Функция определена и непрерывна на всём множестве действительных чисел, кроме
. В этой точке функция имеет разрыв. Найдём односторонние пределы функции при
:

.

Так как данная функция в точке
имеет конечные односторонние пределы, не равные друг другу, то эта точка является точкой разрыва первого рода. Скачок функции в точке
равен .

Вопросы для самоконтроля знаний

Что называется приращением аргумента и приращением функции?

Что называется левосторонним (левым) пределом функции?

Что называется правосторонним (правым) пределом функции?

Какая функция называется непрерывной в точке, в интервале?

Какая точка называется точкой разрыва функции?

Какая точка называется точкой разрыва первого рода?

Какая точка называется точкой разрыва второго рода?

Какая точка называется точкой устранимого разрыва?

Задания для самостоятельной работы

Исследовать функции на непрерывность:

в точке
.

Определение. Пусть на некотором промежутке определена функция f(x) и x 0 – точка этого промежутка. Если , то f(x) называется непрерывной в точке x 0 .
Из определения следует, что о непрерывности можно говорить лишь по отношению к тем точкам, в которых f(x) определена (при определении предела функции такого условия не ставилось). Для непрерывных функций , то есть операции f и lim перестановочны. Соответственно двум определениям предела функции в точке можно дать два определения непрерывности – «на языке последовательностей» и «на языке неравенств» (на языке ε-δ). Предлагается это сделать самостоятельно.
Для практического использования иногда более удобно определение непрерывности на языке приращений.
Величина Δx=x-x 0 называется приращением аргумента, а Δy=f(x)-f(x 0) – приращением функции при переходе из точки x 0 в точку x.
Определение. Пусть f(x) определена в точке x 0 . Функция f(x) называется непрерывной в точке x 0 , если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть Δy→0 при Δx→0.

Пример №1 . Доказать, что функция y=sinx непрерывна при любом значении x .
Решение. Пусть x 0 – произвольная точка. Придавая ей приращение Δx, получим точку x=x 0 +Δx. Тогда Δy=f(x)-f(x 0) = sin(x 0 +Δx)-sin(x) = . Получаем .

Определение . Функция y=f(x) называется непрерывной в точке x 0 справа (слева), если
.
Функция, непрерывная во внутренней точке, будет одновременно непрерывной справа и слева. Справедливо и обратное утверждение: если функция непрерывна в точке слева и справа, то она будет непрерывной в этой точке. Однако функция может быть непрерывной только с одной стороны. Например, для , , f(1)=1, следовательно, эта функция непрерывна только слева (график этой функции см. выше в пункте 5.7.2).
Определение. Функция называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка.
В частности, если промежутком является отрезок , то на его концах подразумевается односторонняя непрерывность.

Свойства непрерывных функций

1. Все элементарные функции непрерывны в своей области определения.
2. Если f(x) и φ(x), заданные на некотором промежутке, непрерывны в точке x 0 этого промежутка, то в этой точке будут также непрерывны функции .
3. Если y=f(x) непрерывна в точке x 0 из X, а z=φ(y) непрерывна в соответствующей точке y 0 =f(x 0) из Y, то и сложная функция z=φ(f(x)) будет непрерывной в точке x 0 .

Разрывы функции и их классификация

Признаком непрерывности функции f(x) в точке x 0 служит равенство , которое подразумевает наличие трех условий:
1) f(x) определена в точке x 0 ;
2) ;
3) .
Если хотя бы одно из этих требований нарушено, то x 0 называют точкой разрыва функции. Другими словами, точкой разрыва называется точка, в которой эта функция не является непрерывной. Из определения точек разрыва следует, что точками разрыва функции являются:
а) точки, принадлежащие области определения функции, в которых f(x) теряет свойство непрерывности,
б) точки, не принадлежащие области определения f(x), которые являются смежными точками двух промежутков области определения функции.
Например, для функции точка x=0 есть точка разрыва, так как функция в этой точке не определена, а функция имеет разрыв в точке x=1, являющейся смежной для двух промежутков (-∞,1) и (1,∞) области определения f(x) и не существует.

Для точек разрыва принята следующая классификация.
1) Если в точке x 0 имеются конечные и , но f(x 0 +0)≠f(x 0 -0), то x 0 называется точкой разрыва первого рода , при этом называют скачком функции .

Пример 2. Рассмотрим функцию
Разрыв функции возможен только в точке x=2 (в остальных точках она непрерывна как всякий многочлен).
Найдем , . Так как односторонние пределы конечны, но не равны друг другу, то в точке x=2 функция имеет разрыв первого рода. Заметим, что , следовательно функция в этой точке непрерывна справа (рис. 2).
2) Точками разрыва второго рода называются точки, в которых хотя бы один из односторонних пределов равен ∞ или не существует.

Пример 3. Функция y=2 1/ x непрерывна для всех значений x, кроме x=0. Найдем односторонние пределы: , , следовательно x=0 – точка разрыва второго рода (рис. 3).
3) Точка x=x 0 называется точкой устранимого разрыва , если f(x 0 +0)=f(x 0 -0)≠f(x 0).
Разрыв «устраним» в том смысле, что достаточно изменить (доопределить или переопределить) значение функции в этой точке, положив , и функция станет непрерывной в точке x 0 .
Пример 4. Известно, что , причем этот предел не зависит от способа стремления x к нулю. Но функция в точке x=0 не определена. Если доопределим функцию, положив f(0)=1, то она окажется непрерывной в этой точке (в остальных точках она непрерывна как частное непрерывных функций sinx и x).
Пример 5. Исследовать на непрерывность функцию .
Решение. Функции y=x 3 и y=2x определены и непрерывны всюду, в том числе и в указанных промежутках. Исследуем точку стыка промежутков x=0:
, , . Получаем, что , откуда следует, что в точке x=0 функция непрерывна.
Определение. Функция, непрерывная на промежутке за исключением конечного числа точек разрыва первого рода или устранимого разрыва, называется кусочно-непрерывной на этом промежутке.

Примеры разрывных функций

Пример 1. Функция определена и непрерывна на (-∞,+∞) за исключением точки x=2. Определим тип разрыва. Поскольку и , то в точке x=2 разрыв второго рода (рис. 6).
Пример 2. Функция определена и непрерывна при всех x, кроме x=0, где знаменатель равен нулю. Найдем односторонние пределы в точке x=0:
Односторонние пределы конечны и различны, следовательно, x=0 – точка разрыва первого рода (рис. 7).
Пример 3. Установить, в каких точках и какого рода разрывы имеет функция
Эта функция определена на [-2,2]. Так как x 2 и 1/x непрерывны соответственно в промежутках [-2,0] и , то разрыв может быть только на стыке промежутков, то есть в точке x=0. Поскольку , то x=0 является точкой разрыва второго рода.

Пример 4. Можно ли устранить разрывы функций:
а) в точке x=2;
б) в точке x=2;
в) в точке x=1?
Решение. О примере а) сразу можно сказать, что разрыв f(x) в точке x=2 устранить невозможно, так как в этой точке бесконечные односторонние пределы (см. пример 1).
б) Функция g(x) хотя имеет конечные односторонние пределы в точке x=2

(,),

но они не совпадают, поэтому разрыв также устранить нельзя.
в) Функция φ(x) в точке разрыва x=1 имеет равные односторонние конечные пределы: . Следовательно, разрыв может быть устранен переопределением функции в точке x=1, если положить f(1)=1 вместо f(1)=2.

Пример №5 . Показать, что функция Дирихле

разрывна в каждой точке числовой оси.
Решение. Пусть x 0 – любая точка из (-∞,+∞). В любой ее окрестности найдутся как рациональные, так и иррациональные точки. Значит, в любой окрестности x 0 функция будет иметь значения, равные 0 и 1. В таком случае не может существовать предела функции в точке x 0 ни слева, ни справа, значит функция Дирихле в каждой точке числовой оси имеет разрывы второго рода.

Пример 6. Найти точки разрыва функции

и определить их тип.
Решение. Точками, подозрительными на разрыв, являются точки x 1 =2, x 2 =5, x 3 =3.
В точке x 1 =2 f(x) имеет разрыв второго рода, так как
.
Точка x 2 =5 является точкой непрерывности, так как значение функции в этой точке и в ее окрестности определяется второй строкой, а не первой: .
Исследуем точку x 3 =3: , , откуда следует, что x=3 – точка разрыва первого рода.

Для самостоятельного решения.
Исследовать функции на непрерывность и определить тип точек разрыва:
1) ; Ответ: x=-1 – точка устранимого разрыва;
2) ; Ответ: Разрыв второго рода в точке x=8;
3) ; Ответ: Разрыв первого рода при x=1;
4)
Ответ: В точке x 1 =-5 устранимый разрыв, в x 2 =1 – разрыв второго рода и в точке x 3 =0 - разрыв первого рода.
5) Как следует выбрать число A, чтобы функция

была бы непрерывной в точке x=0?
Ответ: A=2.
6) Можно ли подобрать число A так, чтобы функция

была бы непрерывной в точке x=2?
Ответ: нет.

Пусть точка a принадлежит области задания функции f(x) и любая ε -окрестность точки a содержит отличные от a точки области задания функции f(x) , т.е. точка a является предельной точкой множества {x} , на котором задана функция f(x) .

Определение . Функция f(x) называется непрерывной в точке a , если функция f(x) имеет в точке a предел и этот предел равен частному значению f(a) функции f(x) в точке a .

Из этого определения имеем следующее условие непрерывности функции f(x) в точке a :

Так как , то мы можем записать

Следовательно, для непрерывной в точке a функции символ предельного перехода и символ f характеристики функции можно менять местами.

Определение . Функция f(x) называется непрерывной справа (слева) в точке a , если правый (левый) предел этой функции в точке a существует и равен частному значению f(a) функции f(x) в точке a .

Тот факт, что функция f(x) непрерывна в точке a справа записывают так:

А непрерывность функции f(x) в точке a слева записывают как:

Замечание . Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва этой функции.

Теорема . Пусть на одном и том же множестве заданы функции f(x) и g(x) , непрерывные в точке a . Тогда функции f(x)+g(x) , f(x)-g(x) , f(x) · g(x) и f(x)/g(x) - непрерывны в точке a (в случае частного нужно дополнительно требовать g(a) ≠ 0 ).

Непрерывность основных элементарных функций

1) Степенная функция y=x n при натуральном n непрерывна на всей числовой прямой.

Сначала рассмотрим функцию f(x)=x . По первому определению предела функции в точке a возьмем любую последовательность {x n } , сходящуюся к a , тогда соответствующая последовательность значений функций {f(x n)=x n } также будет сходиться к a , то есть , то есть функция f(x)=x непрерывная в любой точек числовой прямой.

Теперь рассмотрим функцию f(x)=x n , где n - натуральное число, тогда f(x)=x · x · … · x . Перейдем к пределу при x → a , получим , то есть функция f(x)=x n непрерывна на числовой прямой.

2) Показательная функция.

Показательная функция y=a x при a>1 является непрерывной функцией в любой точке бесконечной прямой.

Показательная функция y=a x при a>1 удовлетворяет условиям:

3) Логарифмическая функция.

Логарифмическая функция непрерывна и возрастает на всей полупрямой x>0 при a>1 и непрерывна и убывает на всей полупрямой x>0 при 0, причем

4) Гиперболические функции.

Гиперболическими функциями называются следующие функции:

Из определения гиперболических функции следует, что гиперболический косинус, гиперболический синус и гиперболический тангенс заданы на всей числовой оси, а гиперболический котангенс определен всюду на числовой оси, за исключением точки x=0 .

Гиперболические функции непрерывны в каждой точке области их задания (это следует из непрерывности показательной функции и теоремы об арифметических действиях).

5) Степенная функция

Степенная функция y=x α =a α log a x непрерывна в каждой точке открытой полупрямой x>0 .

6) Тригонометрические функции.

Функции sin x и cos x непрерывны в каждой точке x бесконечной прямой. Функция y=tg x (kπ-π/2,kπ+π/2) , а функция y=ctg x непрерывна на каждом из интервалов ((k-1)π,kπ) (здесь всюду k - любое целое число, т.е. k=0, ±1, ±2, …) .

7) Обратные тригонометрические функции.

Функции y=arcsin x и y=arccos x непрерывны на отрезке [-1, 1] . Функции y=arctg x и y=arcctg x непрерывны на бесконечной прямой.

Два замечательных предела

Теорема . Предел функции (sin x)/x в точке x=0 существует и равен единице, т.е.

Этот предел называется первым замечательным пределом .

Доказательство . При 0 справедливы неравенства 0<\sin x. Разделим эти неравенства на sin x , тогда получим

Эти неравенства справедливы также и для значений x , удовлетворяющих условиям -π/2. Это следует из того, что cos x=cos(-x) и . Так как cos x - непрерывная функция, то . Таким образом, для функций cos x , 1 и в некоторой δ -окрестности точки x=0 выполняются все условия теорем. Следовательно, .

Теорема . Предел функции при x → ∞ существует и равен числу e :

Этот предел называется вторым замечательным пределом .

Замечание . Верно также, что

Непрерывность сложной функции

Теорема . Пусть функция x=φ(t) непрерывна в точке a , а функция y=f(x) непрерывна в точке b=φ(a) . Тогда сложная функция y=f[φ(t)]=F(t) непрерывна в точке a .

Пусть x=φ(t) и y=f(x) - простейшие элементарные функции, причем множество значений {x} функции x=φ(t) является областью задания функции y=f(x) . Как мы знаем, элементарные функции непрерывны в каждой точке области задания. Поэтому по предыдущей теореме сложная функция y=f(φ(t)) , то есть суперпозиция двух элементарных функций, непрерывна. Например, функция непрерывна в любой точке x ≠ 0 , как сложная функция от двух элементарных функций x=t -1 и y=sin x . Также функция y=ln sin x непрерывна в любой точке интервалов (2kπ,(2k+1)π) , k ∈ Z (sin x>0 ).

Читайте также...

• Традиционные общества Востока в раннее Новое время
• Классификация гласных и согласных звуков
• Вероятностно-статистические методы исследований Вероятностно статистические методы
• Воронежский государственный архитектурно-строительный университет Воронежский государственный строительный